PG ou progressão geométrica é uma sequência numérica em que os números, a partir do segundo, são obtidos multiplicando seu antecessor por uma constante q, que chamamos de razão. Portanto, a razão ou divisão entre dois termos quaisquer e consecutivos de uma PG é uma constante. Nesse sentido, para calcular a razão de uma PG basta dividir um número pelo seu antecessor.
Índice
- Exemplos de progressão geométrica
- Tipos de PG
- Como calcular a razão de uma PG
- Termo geral de uma PG
- Soma dos termos de uma PG
- Soma dos termos de uma PG infinita
- Produto dos termos de uma PG
- Propriedades de uma PG
Exemplos de progressão geométrica
Observe as sequências geométricas abaixo:
- (3, 6, 12, 24, 48) é uma PG finita, crescente e razão q = 2.
- (2, 6, 18, 54, 162) finita, crescente e razão q = 3.
- (100, 50, 25, 12,5, 6,25, …) infinita, decrescente e razão q = 0,5.
- (1, -5, 25, -125, 625) finita, oscilante e razão q = -5.
Tipos de progressão geométrica
- Crescente: cada termo da PG será maior que seu antecessor. Exemplos:
- (2, 8, 32, 128) com q = 4
- (-8, -4, -2, -1) com q = 1⁄2
- Decrescente: cada termo da PG é menor que seu antecessor. Exemplos:
- ( -4, -16, -64, 256) com q = 4
- (64, 32, 16, 8) com q = 1⁄2
- Constante: todos os termos da PG são iguais, nesse caso q = 1. Exemplos:
- (7, 7, 7, 7) com q = 1
- ( -3, -3, -3, -3) com q = 1
- Oscilante: todos os termos da PG são intercalados entre positivo e negativo. Situação indicativa de razão negativa (q<0). Exemplos:
- ( -5, 5, -5, 5) com q = -1
- ( 1,-3, 9, -27) com q = -3
Como calcular a razão de uma PG
A razão da PG é dada pela divisão de um termo qualquer, exceto o primeiro termo, pelo termo anterior. Com isso, temos a fórmula da razão da PG.

Termo geral de uma PG
Podemos encontrar qualquer termo geral de uma PG ou o total de termos utilizando a fórmula:
- an = a1 . q(n – 1)
Em que:
- an: é o termo geral;
- a1: é o primeiro termo;
- n: é o número de termos;
- q: é a razão.
Observe a explicação de como foi feita a fórmula.
Considere uma PG de razão q:
- (a1, a2, a3, …, an, …)
A partir da sequência acima sabemos que:
- a2 = a1 . q
- a3 = a2 . q
- a4 = a3 . q
- …
- an = an-1 . q
Se multiplicarmos as igualdades acima, membro a membro, teremos:
(a2 . a3 . a3 . … . an-1) . an = a1 . (a2 . a3 . … an-1) . q . q . q . … + q ((n – 1) vezes)
Após simplificarmos os termos, chegamos a fórmula:
- an = a1 . q(n – 1)
Exemplo:
- Determine o 10º (décimo) termo de uma PG sabendo que a1 = 2 e q = 3.
Nesse caso, vamos utilizar a fórmula do termo geral da PG. Temos que: a1 = 2, q = 3 e n = 10 Dessa forma: a10 = 2 . 3(10 – 1) a10 = 2 x 39 a5 = 2 x 19683 = 39366.
Soma dos termos de uma PG
Podemos calcular a soma dos n termos de uma progressão geométrica a partir da fórmula:

Sn : Soma dos n termos da PG
a1 : primeiro termo da sequência
q : razão
n: quantidade de elementos da PG
Exemplo:
Calcule a soma dos 5 primeiros termos da PG (1, 3, 9,…).
Extraímos a informação que a1 = 1, q = 3 e n = 5

Soma dos termos de uma PG infinita
Podemos calcular a soma dos termos de uma progressão geométrica infinita quando a razão q for um número entre -1 e 1. Nesses casos, a expressão qn acaba convergindo para 0.
Logo, temos a seguinte fórmula:
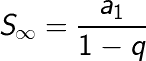
Lembrando que essa fórmula só se aplica quando a razão q estiver entre -1 e 1.
Produto dos termos de uma PG
Podemos calcular o produto dos n termos de uma PG. Para isso utilize a fórmula:

Propriedades de uma PG
1 – o quadrado do termo médio é igual ao produto dos extremos. Por exemplo: considere a PG (1, 5, 25, 75…). Nesse caso, 5²=1.25 e 25²=5.75.
2 – O produto dos termos equidistantes dos extremos de uma PG é igual ao produto desses extremos. Por exemplo: considere a PG (a, b, c, d, e, f, …). Nesse caso, a.f=b.e=c.d
