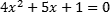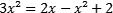As equações do 2º grau são caracterizadas por possuírem uma incógnita que permite duas raízes, que podem ser diferentes ou iguais. As raízes são as respostas da equação. Dado um problema, dizemos que se trata de uma equação do 2º grau quando a equação puder ser reduzida na seguinte forma:

Diferente da equação do 1º grau, agora a incógnita aparece duas vezes. Dizemos que é uma equação do 2º grau porque tem uma incógnita elevada ao quadrado. Na forma geral da equação, ‘a’, ‘b’ e ‘c’ são constantes que incluem frações, números negativos e números com vírgula. A condição para que seja considerada equação do 2º grau é que a constante ‘a’ seja diferente de zero.
Equação do 2º grau completa
Uma equação do 2º grau é completa quando as incógnitas ‘b’ e ‘c’ são diferentes de zero, assim como a incógnita ‘a’.
Exemplo de equação do 2º grau completa
![]()
A equação acima se trata de uma equação do 2º grau completa porque as incógnitas ‘b’ e ‘c’ são diferentes de zero. ‘b’ vale 5 e ‘c’ vale -6.
Equação do 2º grau incompleta
Para que uma equação do 2º grau seja incompleta, pelo menos uma das incógnitas, ‘b’ ou ‘c’, tem que ser igual a zero.
Exemplos de equações do 2º grau incompleta
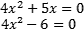
Ambas as equação do 2º grau acima são incompletas. Na primeira porque a incógnita ‘c’ é igual a zero e na segunda porque a incógnita ‘b’ é igual a zero.
As equações do 2º grau incompletas podem ser resolvidas sem utilizar a fórmula de Bhaskara. Veremos todos esses métodos adiante.
Fórmula de Bhaskara
A fórmula de Bhaskara é a forma mais conhecida de resolver equações do 2º grau, completas e incompletas. Pode ser considerada a fórmula geral da equação do 2º grau, pois é possível aplica-la em qualquer equação do 2º grau.

Utilizando essa fórmula, você resolve todas as equações do 2º grau. Observe que na fórmula existe o sinal de mais ou menos. A primeira raiz você utiliza o sinal de mais e para resolver a segunda raiz você usa o sinal de menos.
Como Resolver com Soma e Produto
Uma forma interessante de resolver equações do 2º grau é utilizando o método soma e produto. Para que a soma e produto funcione é preciso que seja satisfeitos as seguintes condições:

Se conseguir encontrar as duas raízes que satisfaça, cumulativamente, essas duas condições, pronto. Exercício resolvido. Aliás, essa é uma técnica viável quando se trata de números inteiros e como na maioria dos exercícios as raízes são números inteiros, então vale tentar por soma e produto antes de resolver por Bhaskara.
Exemplo de resolução de equação do 2º grau usando soma e produto
Considere a equação: x²-6x+8=0. Vamos começar pensando em dois números cujo produto seja igual a 8 e depois vamos verificar se a soma é igual a 6. Como é um número pequeno, vamos tentar com números pequenos.
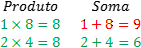
Portanto, as raízes dessa equação são 6 e 8.
Resolvendo equações do 2º grau incompletas
Como disse anteriormente, as equações do 2º grau incompletas possuem maneiras mais simples de serem resolvidas.
Quando ‘b’=0
Nesses casos, basta isolar a incógnita de um lado da equação e passar todas as constantes para o outro lado. Feito isso, extraímos as raízes. A fórmula é:

Quando ‘c’=0
Nesses casos, uma das raízes sempre será zero. A outra raiz é dada pela fórmula:
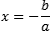
Quando ‘b’=0 e ‘c’=0
Nesse caso, a raiz é única e vale zero.
Delta da equação do 2º grau
O delta (Δ) é muito útil para analisar o comportamento de uma equação do 2º grau. O delta, inclusive, faz parte da fórmula de Bhaskara. A fórmula do delta é:

O resultado de delta pode ter 3 significados:
- Δ<0, delta menor do que zero: significa que não existem raízes reais;
- Δ=0, delta igual a zero: significa que existem duas raízes reais iguais;
- Δ>0, delta maior do que zero:significa que existem duas raízes reais distintas.
Exercícios de equações do 2º grau